![[PukiWiki]](image/blackuni3-80x80.png "[PukiWiki]")
工事中
VSCode で Markdown のファイルを作ってみましょう．
# 大きい見出しです ## 中くらいの見出しですです 行の先頭を `#` や `##` で始めると，章や節のタイトルになります． 「大きい見出しです」は `#` で，「中くらいの見出しですです」は，`##` で始まってるので，前者よりも後者の方が一つ下のレベルの見出しとなっています． ほげほげほげほげほげほげほげほげほげほげほげほげほげほげほげほげほげほげほげほげ ほげほげほげほげほげほげほげほげほげほげほげほげほげほげほげほげほげほげほげほげ． ## 中くらいの見出しでんがなまんがな 「中くらいの見出しでんがなまんがな」は，「〜ですです」と同じレベルのタイトルですです． ### も一つ下の見出しでっせ `###` にすると↑のようになります． だんらくだんらくだんらくだんらくだんらく *だんらく* だんらくだん **らくだ** んらくだんらくだんらくだんらくだんらくだんらくだんらくだんらくだんらくだんらくだんらくだんらくだんらくだんらくだんらくだんらく． だんらくだんらくだんらくだんらく．
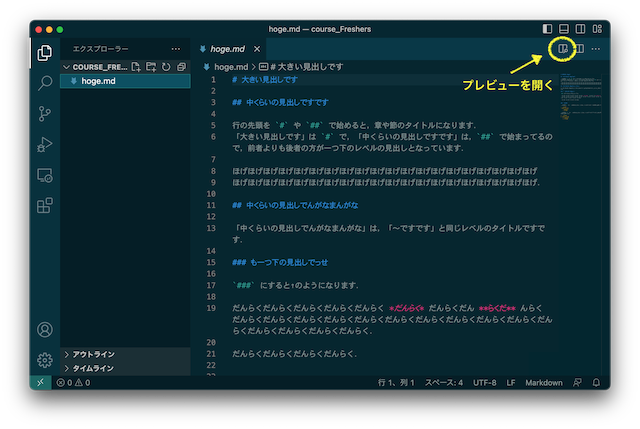
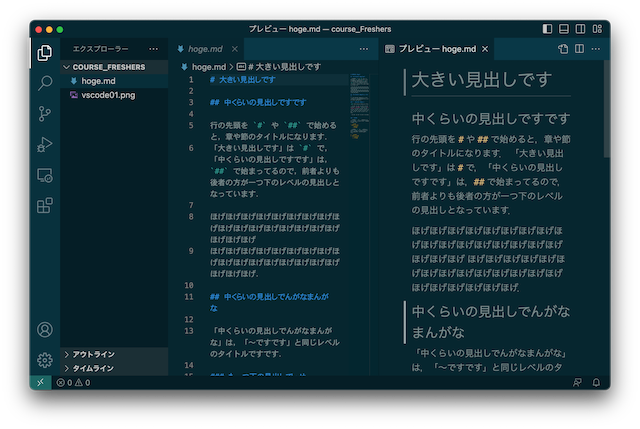
hoge.md の末尾に以下を追加して観察しましょう．
### 箇条書き
行の先頭を`- `（`-` のあとに半角の空白を入れる）とすると，箇条書きができます．
- 箇条書き
- かじょーがき
- 過剰牡蠣
- 渦状柿
行の先頭を `1. `（`.` のあとに半角の空白を入れる）とすると，すると，番号付きの箇条書きができます．
1. 箇条書き
1. かじょーがき
1. 過剰牡蠣
1. 渦状柿
工事中
VSCode では，Markdown 文書中に LaTeX記法 で数式を書いたものをプレビューできます．
hoge.md の末尾に以下を追加して観察しましょう．
# Markdown に LaTeX 数式を書く
Markdown を扱えるソフトの中には，「LaTeX 記法」で書いた数式を整形してプレビューできるものも多くあります．
VSCode もその一つです．
## 文の中に数式を入れる
以下の文中の `$` と `$` で囲まれた部分が，LaTeX記法で書いた数式です．
$x$ に関する二次方程式 $ax^2 + bx + c = 0$ の解は，$a \ne 0$ のとき，$x = \frac{-b \pm \sqrt{b^2-4ac} }{2a}$ である．
$n$ を任意の自然数として，$\sum_{k=1}^{n}k = \frac{n}{2}(n+1)$ が成り立つ．
$f(x) = e^{-x^2}$ のとき，$\int_{-\infty}^{\infty}f(x)dx = \sqrt{\pi}$ である．
さらに以下を追加して観察しましょう．
## 独立した数式を書く
長い数式を書きたい場合，`$$` と `$$` で囲みます．新たな行に独立した数式として表されます．
$n$ を任意の自然数として，
$$ \sum_{k=1}^{n}k = \frac{n}{2}(n+1) $$
が成り立ちます．
$f(x) = e^{-x^2}$ のとき，
$$\int_{-\infty}^{\infty}f(x)dx = \sqrt{\pi}$$
である．
さらにさらに以下を追加して観察しましょう．
## 補足
LaTeX 記法については，Google等の検索エンジンで「latex ほげほげ」のようなキーワードで検索すれば，たくさん情報が出てきます．
- LaTeX で書けるもの全てが Markdown 上に書けるわけではありません．
- Markdown にもいろいろ方言があるので，VSCode で書いてプレビューできる LaTeX 記法が，他のソフトでエラーになることもたまにあります．
`$$` で囲む別行立て数式の場合，次のように `\begin{alinged}...\end{aligned}` を使うと複数行に渡る数式をいい感じに揃えられます（詳しくは「latex aligned」等で検索してね ）．
$$
\begin{aligned}
\int_{1}^{2}(x^2 - 2x + 1 )dx &= \int_1^2 (x-1)^2dx \\
&= \left[ \frac{(x-1)^3}{3} \right]_1^2 \\
&= \frac{1}{3}
\end{aligned}
$$
$x_1, x_2, \ldots, x_N$ の平均を $\bar{x}$ とおくとき，$y_n = x_n + b$ の平均 $\bar{y}$ は
$$
\begin{aligned}
\bar{y} &=\frac{1}{N}\sum_{n=1}^{N}y_n \\
&= \frac{1}{N} \sum_{n=1}^{N}(x_n+b) \\
&= \frac{1}{N}\sum_{n=1}^{N}x_n + \frac{1}{N}\sum_{n=1}^{N}b \\
&= \bar{x} + \frac{1}{N}\times bN \\
&= \bar{x} + b
\end{aligned}
$$
となる．
