応用プログラミング及び実習 2019年度 第5回 実習課題S¶
- AProgのページ https://www-tlab.math.ryukoku.ac.jp/wiki/?AProg/2019
- 第5回のページ https://www-tlab.math.ryukoku.ac.jp/wiki/?AProg/2019/ex05
おまけ課題です. 分からないところがあれば随時 takataka に相談してください.
ねらい¶
この課題のねらいは次のようなものです:
多変量解析(多次元のデータを統計的に分析する手法)の一つである,主成分分析(PCA: Principal Component Analysis) について簡単に学び,体験してみる
Step1 準備,データの読み込み¶
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
まずは,以下のリンク先のファイルをこの notebook と同じ場所に保存しましょう: https://www-tlab.math.ryukoku.ac.jp/~takataka/course/AProg/mpi100.csv
less コマンドで内容を確認しましょう.このファイルには,「数学」,「物理」,「情報」3科目の点数が100人分格納されています.
読み込んでみましょう.
# テキストファイルを読み込んで NumPy の配列に格納.
hoge = np.loadtxt("mpi100.csv", delimiter=",", skiprows=1)
X = hoge[:, 1:] # 最初の列はデータ番号なので捨てる
変数 X の内容を確認してみましょう.
print(X)
X.shape
X は2次元配列であることがわかりますね.
Step2 平均とヒストグラム¶
データの性質を調べるとしたら,まずは平均からでしょうか.平均値は...
xm = np.mean(X, axis = 0)
xm
左から順に,「数学」,「物理」,「情報」の平均点.
ヒストグラムも描いてみましょう.
### 3つのヒストグラムを並べる
fig = plt.figure(figsize=(10,3))
ax1 = fig.add_subplot(131)
ax2 = fig.add_subplot(132)
ax3 = fig.add_subplot(133)
# 0列目,「数学」
ax1.set_title("Mathematics")
ax1.set_xlim([0,100])
ax1.set_ylim([0,30])
ax1.hist(X[:, 0])
# 1列目,「物理」
ax2.set_title("Physics")
ax2.set_xlim([0,100])
ax2.set_ylim([0,30])
ax2.hist(X[:, 1])
# 2列目,「情報」
ax3.set_title("Information")
ax3.set_xlim([0,100])
ax3.set_ylim([0,30])
ax3.hist(X[:, 2])
fig.tight_layout()
上記の平均値が納得できる分布してるようです.
Step3 分散共分散行列と散布図¶
このデータは,一人分が3科目の点数を表す3つの数値の組でできています.これらを 3 次元ベクトルとして扱うことにして, $$ \mathbf{x}_{n} = \begin{pmatrix} m_n \\ p_n \\ i_n \end{pmatrix}$$ と書くことにしてみます.$n = 1, 2, \dots , N$ はデータの番号(いまの場合は $N=100$)で,$m_{n}, p_{n}, i_n$ は $n$ 番目のひとの「数学」,「物理」,「情報」それぞれの点数.
このデータの平均を $\bar{\mathbf{x}}$ と表記することにすると, $$ \bar{\mathbf{x}} = \frac{1}{N}\sum_{n=1}^{N}\mathbf{x}_{n} $$ となります.このとき,次式で定まる行列 $V$ をこのデータの分散共分散行列 といいます. $$ V = \frac{1}{N}\sum_{n=1}^{N} (\mathbf{x}_{n} - \bar{\mathbf{x}})(\mathbf{x}_{n} - \bar{\mathbf{x}})^{\top}$$ データの次元数を $D$ とすると,$V$ は $D\times D$ 行列になります.いまの例では $D=3$.
NumPy 使って計算してみましょう.
N, D = X.shape # いまのデータの場合, N = 100, D = 3
XX = X - xm # 平均を引いたデータ. N x D 行列
print(XX.shape)
V = XX.T @ XX / N # 分散共分散行列を求める
print(V)
定義から明らかですが,$V$ は対称行列です.対角要素は,$D$個の値それぞれの分散.いまの場合,「数学」の分散が約 81, 「物理」の分散が約 122, 「情報」の分散が約 120 ってことです(グラフ見ても,「数学」の散らばりちょっと小さいですね).式で書くと, $$ \frac{1}{N}\sum_{n=1}^{N} (m_n - \bar{m})^2 = 81.0$$ とかそういうことになります.$\bar{m}$ は $m_n$ の平均値.
他方,例えば $(1,2)$ および $(2,1)$ 要素は,「数学」と「物理」の関係を表す量で,式で書くと次のようになります. $$ \frac{1}{N}\sum_{n=1}^{N} (m_n - \bar{m})(p_n - \bar{p}) = -15.6$$ この量は,共分散と呼ばれます.他の非対角要素もそれぞれ対応する2科目間の共分散.
共分散の値は,対象とする2つの量の間にどんな関係があるかによって,符号を含めて変化します.上記の $m_n$ と $p_n$ の共分散は負ですが,この場合,「数学」が平均点より高いひとは「物理」は平均点より低くなりがち,ということを表してます. 他の値も見ると,「数学」と「情報」の間も同様でかつより強くその傾向にあり,「物理」と「情報」の共分散は正ですので,こちらは一方が平均点より高いひとは他方も平均点より高い傾向にある,ということを意味しています.
他の授業で 相関/相関係数 というものを学んだひとは,似たようなことを言ってるな,と思ったかもしれません.実際,相関係数は,共分散を用いて次のように表されます. $$ \mbox{($m_n$と$p_n$の相関係数)} = \frac{\mbox{($m_n$と$p_n$の共分散)}}{\mbox{($m_n$の標準偏差)($p_n$の標準偏差)}}$$
上記で述べた傾向を確認するために,2科目間の関係を散布図に描いて可視化してみましょう.
### 3つの散布図を並べる
fig = plt.figure(figsize=(10,3))
ax1 = fig.add_subplot(131)
ax2 = fig.add_subplot(132)
ax3 = fig.add_subplot(133)
# 「数学」vs「物理」
ax1.set_title("Math-Physics")
ax1.set_xlim([0,100])
ax1.set_ylim([0,100])
ax1.set_aspect("equal")
ax1.scatter(X[:, 0], X[:, 1])
# 「数学」vs「情報」
ax2.set_title("Math-Information")
ax2.set_xlim([0,100])
ax2.set_ylim([0,100])
ax2.set_aspect("equal")
ax2.scatter(X[:, 0], X[:, 2])
# 「物理」vs「情報」
ax3.set_title("Physics-Information")
ax3.set_xlim([0,100])
ax3.set_ylim([0,100])
ax3.set_aspect("equal")
ax3.scatter(X[:, 1], X[:, 2])
fig.tight_layout()
共分散の値が小さい(負で絶対値が大きい)「数学」vs「情報」は右下がりに分布しており,一方の点数が良いと他方の点数が悪い傾向にあることが読み取れますね.
Step4 主成分分析とは¶
主成分分析の目的は,上記の例のような多次元のデータが与えられたときに,このデータの散らばりを説明できるような軸を見つけることです.もう少し真面目な言い方をすると,データから複数の互いに「無関係」な因子を取り出し,個々のデータをこれらの因子の線形結合で表すことが目的です.
簡単のためここでは,軸を1つだけ見つける(因子を1つだけ取り出す)場合について説明します.
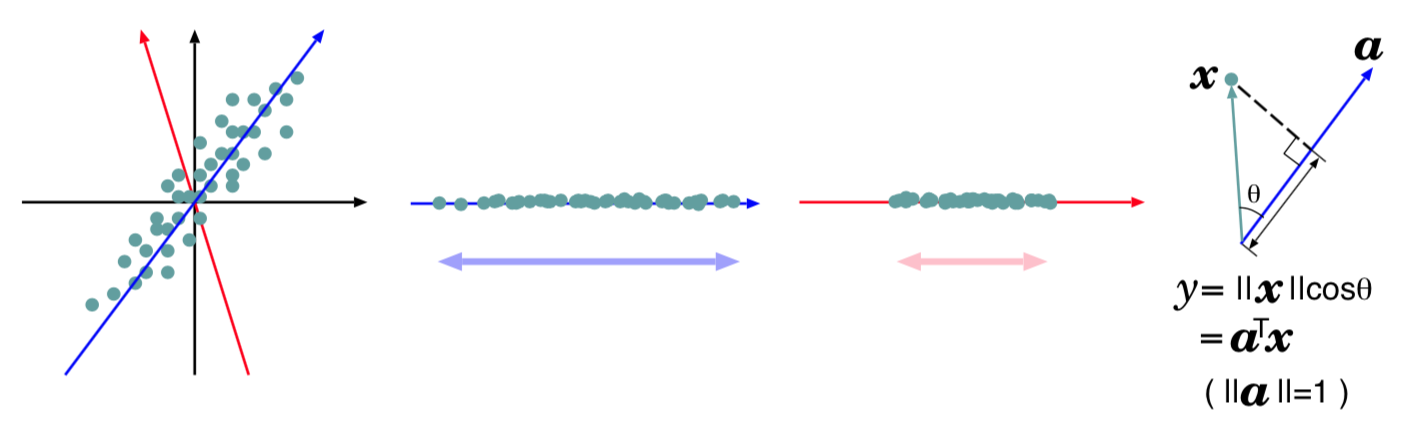
上図左の灰色の点たちは,データから平均を引いたもの $\mathbf{x}_n - \bar{\mathbf{x}} (n = 1, 2, \dots , N )$ です.図を描くため,データが2次元と仮定してます. これらのデータを青い軸方向の成分のみで説明し ようとすると,その成分は左から 2 番目の図のように散らばるでしょう. 赤い軸方向の成分のみだと,左から 3 番目の図のように散らばるでしょう. この二つを見比べると,青い軸方向の方がデータがより散らばっており,元データの多様性をより表現できている気がしませんか?
直感的な説明ですが,このような観点から,主成分分析では,元データを表す軸として,その方向に測った分散がより大きくなるようなものを選びます. 右端の図は,選んだ軸が $\mathbf{a}$ という単位ベクトル方向だったときに,元データ $\mathbf{x}$ と,それをこの方向に見た(射影した)量 $y$ との間の関係を図示しています. 元データ $\mathbf{x}$ は2多次元だけど, $y$ を計算して $y$ だけ眺めても元データの様子がわかるんじゃね? というわけ.
一般化して主成分分析の目的をもう一度言い直すと,$D$次元データから,その散らばりをよく説明する少数の基底ベクトルを見つけて,その線形結合でデータを表すこと,ということになります. データの次元数 $D$ が大きいときに,それをより少ない次元数で表してみよう,ということ.
この主成分分析については,数理情報学科3年前期科目「パターン情報処理」の 2019年度第15回講義資料 p.4 と p.5 でもちょこっと説明と,あと猫の顔画像への応用例を書いてます.
で,目的にかなう「軸」/「因子」/「基底」はどうやって見つけるかというと,実は,データの分散共分散行列の固有ベクトルでよい,ということが知られています (部分的な証明が上記講義資料中にあります). 1つだけで良いなら,最大固有値に対応した固有ベクトル,複数必要なら,対応する固有値の大きい方から順に.
もう少しちゃんと説明すると, 固有値を降順に番号付け,つまり $$ \lambda_1 \ge \lambda_2 \ge \dots \lambda_D $$ とし,固有ベクトルにも対応する固有値と同じ番号を付けることにして $$ \mathbf{u}_1, \mathbf{u}_2, \dots \mathbf{u}_D $$ とします.このとき,固有値は対応する固有ベクトルの方向の分散を表しており, 番号の小さい固有ベクトルほど,元のデータで分散のより大きい方向を向いているます.すなわち,番号の小さい固有ベクトルほど元データをよく説明する因子となっています.
Step5 主成分分析やってみよう¶
ごたくはこの辺にして,ここからは実際に計算しながら説明します. まずは,$V$の固有値固有ベクトルを求めます.
u, s, v = np.linalg.svd(V) # 特異値分解(今の条件ではこれで固有値固有ベクトルが求まる)
eva = s # V の固有値
eve = v # V の固有ベクトルをならべた行列, eve[0] が最大固有値に対応した固有ベクトル,eve[1] が2番目,...
for i in range(D):
print(f"{i}番目の固有値:{eva[i]:.2f}\t固有ベクトル: {eve[i]}")
いまの例では $D=3$ ですので,固有値固有ベクトルは 3 通りあります.
データ $\mathbf{x}$ に対して, $$ y_i = \mathbf{u}_i \cdot (\mathbf{x} - \bar{\mathbf{x}})$$ を $\mathbf{x}$ の「第$i$主成分スコア」といいます($\bar{\mathbf{x}}$はデータの平均).この $y_i$ の値は,$\mathbf{u}_{i}$ ($i$番目に「重要」な因子)の軸に沿ってこのデータが平均からどのくらいずれているかを表します.
# 主成分スコアを求めてみる
Y = XX @ eve.T # XX はデータから平均を引いたもの
print('# 番号 データ(数,物,情) 主成分スコア(第1, 2, 3)')
for n in range(N):
print('{0:>2} ( {1[0]:.0f}, {1[1]:.0f}, {1[2]:.0f} ) ({2[0]: >6.1f}, {2[1]: >6.1f}, {2[2]: >6.1f} )'.format(n, X[n, :], Y[n, :]))
これだけではどうなってるかわかりにくいかもですので,第1主成分スコアでソートしてみましょう.
# 第1主成分スコアで
idx = np.argsort(-Y[:, 0]) # 第1主成分スコアでソートしたデータ番号
print('# 番号 データ(数,物,情) 主成分スコア(第1)')
for n in range(N):
i = idx[n]
print('{0:>2} ( {1[0]:.0f}, {1[1]:.0f}, {1[2]:.0f} ) {2: >6.1f}'.format(i, X[i, :], Y[i, 0]))
これを見ると,第1主成分スコアが大きいひとは「数学」(M)の点数が低くて「物理」(P)と「情報」(I)の点数が高い,という傾向にあることがわかります. そのことは,第1固有ベクトルが以下の値であることからもわかります(このベクトルの各要素をM, P, I にかけて足したものが第1主成分スコアになるのでした).
eve[0]
どうやらこのデータは,「PI得意M苦手 <=> PI苦手M得意」という方向に大きく散らばっているようです. 全部得意とか全部苦手ということはあまり多くなくて,PIかMかどちらかに偏ってるようです.
★★★ 上記と同様に,第2主成分スコア,第3主成分スコアでもソートして結果を眺めてみましょう.
# 第2主成分スコアで
# 第3主成分スコアで
★★★ 元データの散布図を描いているコードを参考にして,主成分スコアの散布図を描いてみましょう.
横軸縦軸の範囲は, [-50, 50] としてください.
### 主成分スコアの散布図
さて,ここで $V$ はどんな中身の行列だったか見てみましょう.
V
これに対して,主成分スコアの分散共分散行列はどうなるでしょう?
まずは式で考えてみましょう.もともと主成分スコアは $$ y_i = \mathbf{u}_i \cdot (\mathbf{x} - \bar{\mathbf{x}})\qquad (i = 1, 2, \dots , D)$$ でしたから,これらをならべた $D$ 次元ベクトル $\mathbf{y}$ は $$ \mathbf{y} =\begin{pmatrix} y_1 \\ \vdots \\ y_D \end{pmatrix} = \begin{pmatrix} \mathbf{u}_{1}^{\top} \\ \vdots \\ \mathbf{u}_{D}^{\top} \end{pmatrix} ( \mathbf{x}- \bar{\mathbf{x}}) = U^{\top} ( \mathbf{x}- \bar{\mathbf{x}}) $$ です.$U$ は固有ベクトルをならべた $D\times D$ 行列. ここから定義通り $\mathbf{y}$ の分散共分散行列を計算すると, \begin{align} \frac{1}{N}\sum_{n=1}^{N} \mathbf{y}_{n}\mathbf{y}_{n}^{\top} &= \frac{1}{N}\sum_{n=1}^{N} U^{\top} ( \mathbf{x}_{n}- \bar{\mathbf{x}}_{n}) \left(U^{\top} ( \mathbf{x}_{n}- \bar{\mathbf{x}}_{n}) \right)^{\top} \\ &= \frac{1}{N}\sum_{n=1}^{N} U^{\top} ( \mathbf{x}_{n}- \bar{\mathbf{x}}_{n}) ( \mathbf{x}_{n}- \bar{\mathbf{x}}_{n})^{\top} U \\ &= U^{\top} \left( \frac{1}{N}\sum_{n=1}^{N} ( \mathbf{x}_{n}- \bar{\mathbf{x}}_{n}) ( \mathbf{x}_{n}- \bar{\mathbf{x}}_{n})^{\top}\right) U \\ &= U^{\top} V U = \begin{pmatrix} \lambda_1 & \dots & 0\\ \vdots & \ddots & \vdots \\ 0 & \dots & \lambda_{D} \\ \end{pmatrix} \end{align} となります($U$が固有ベクトルをならべた行列だったのを思い出しましょう). つまり,主成分分析で得られる主成分スコアは,互いの共分散(相関)が 0 になる,という性質をもっています.
★★★ 元データの分散共分散行列を計算しているところを参考に,Y の分散共分散行列を求めるコードを書きましょう(ヒント: Y は XX に行列 U をかけたものです. XX は平均をすでに引いてありますので,その平均は 0 です.したがって,Y も平均は 0 です).
# 主成分スコア Y の分散共分散行列
正しい結果が出せれば,対角以外の要素は全て 0 (誤差はありますが)になっていること,対角要素が固有値に一致していることがわかります.
Step6 主成分分析とデータ圧縮¶
主成分スコアは,分散の大きさの順に番号が付いています.ちゃんとした説明はしませんが,分散の大きな主成分スコアほど,元のデータの重要な情報を含んでいると考えることができます. 逆に考えると,番号の大きい成分はあまり重要でないといえそうです.
上記の例では,$\mathbf{x}$ は3次元で,主成分スコアも $y_1, y_2, y_3$ の3つ得られます.ここも説明を省略しますが,これらの間には $$ \mathbf{x} - \bar{\mathbf{x}} = y_1\mathbf{u}_1 + y_2\mathbf{u}_2 + y_3\mathbf{u}_3 $$ という関係があります.3番目の成分が重要でないということなら, $$ \tilde{\mathbf{x}} - \bar{\mathbf{x}} = y_1\mathbf{u}_1 + y_2\mathbf{u}_2$$ という値を計算してみると,$\tilde{\mathbf{x}}$ は $\mathbf{x}$ の良い近似になっているかもしれません.
やってみませう.
Y2 = Y[:, :2] # y1, y2 から成る行列
Y2.shape
XXt = Y2 @ eve[:2, :] # Y2 (N x 2) と 第1,第2固有ベクトルをならべた行列 (2 x D) との積
XXt.shape
Xt = XXt + xm # 平均を加える
print('# 番号 データ(数,物,情) 2次元での再構成')
for n in range(N):
print('{0:>2} ( {1[0]:.0f}, {1[1]:.0f}, {1[2]:.0f} ) ({2[0]: >6.1f}, {2[1]: >6.1f}, {2[2]: >6.1f} )'.format(n, X[n, :], Xt[n, :]))
★★★ 上記の結果に納得したら,第2主成分スコアも捨てて第1主成分スコアだけでデータを近似するようにコードを書き換えてみましょう.
主成分分析は,多次元のデータからその本質的な情報を抽出することで,元のデータの次元数($D$)より少ない次元数の情報(主成分スコア)で元データの特徴を表そうとする方法です.上記の例は3次元のデータでしたが,画像のようなデータの場合,次元数は簡単に千とか万なんて数になります(例えば $100\times 100$ 画素のカラー画像まるごとだったら $30000$次元). そのような大規模なデータを扱いたい,分析したい,という場面でもこの主成分分析はよく用いられます.
主成分分析の画像データへの適用例については,数理情報学科3年前期科目「パターン情報処理」の 2019年度第15回講義資料 p.4 と p.5 にちょっとだけあります(猫の顔画像への応用例).